Inertial and rotating frames

Inertial and rotating frames

Anyone who’s ever needed to keep track of an object’s \(x\), \(y\), and \(z\) coordinates can attest that dealing with coordinate frames can be a slog. There can be lots of technical details involved, but luckily there are only two kinds of coordinate frames we really need to understand.

• Non-rotating frames

• Rotating frames

At a basic level, non-rotating frames are also called inertial frames. By default, rotating frames are therefore non-inertial frames.

So what’s the big deal, why make the distinction? It turns out that both kinds of frames have their strengths and weaknesses in astrodynamics.

• Inertial

  • Often centered on celestial bodies/barycenters and stationary relative to the stars

  • Trajectories look “right” (intuitive)

  • Always oriented the same relative to other inertial frames

  • Has time dependence for rotating objects

  • Cannot fully visualize a trajectory relative to a rotating object for all time

• Rotating

  • Trajectories look “wrong” (unintuitive) and initially confusing due to learning curve

  • Orientation relative to an inertial frame is always changing

  • Can fully remove time dependence, such as when used with:

    1. Two bodies in circular orbit

    2. A body-fixed frame

  • Can fully visualize a trajectory relative to a rotating object for all time

Why use a rotating frame?

It turns out that removing time-dependence on the dynamics is a very powerful concept, and for that reason, the majority of work done in the CRTBP is done in the rotating frame.

• “The rotating frame” will always mean the frame that keeps the two bodies aligned on the \(x\) axis

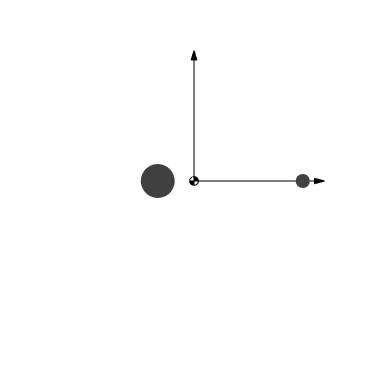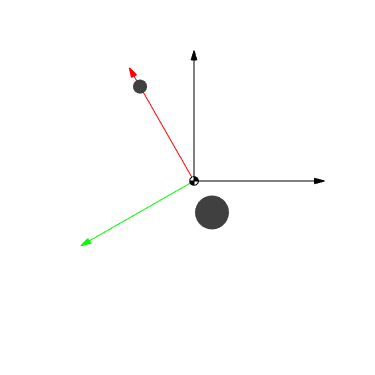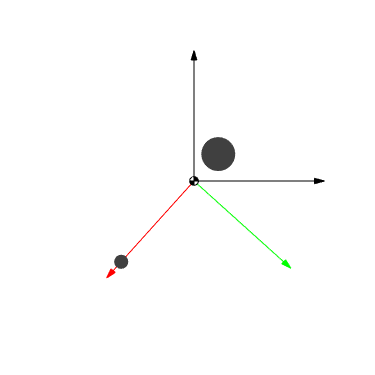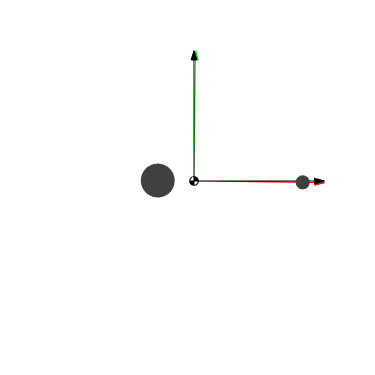
Fig. 2 The inertial frame and the rotating frame. Both frames are centered on the barycenter and are color coded so that they are aligned when the smaller body crosses upwards through the inertial \(x\) axis.

When viewed in the rotating frame, the motion of the two bodies becomes stationary and independent of time.

Fig. 3 In the rotating frame, the two bodies appear stationary for all time.

Trajectories in the inertial and rotating frames

Let’s compare what a trajectory in the CRTBP looks like between the four different options we have:

• Inertial frame relative to the primary

• Inertial frame relative to the secondary

• Inertial frame relative to the barycenter

• Rotating frame relative to the barycenter

In each of the following scenarios, the underlying trajectory is all the same. The only thing that’s changing is how the trajectory is being represented by adjusting the frame and origin.

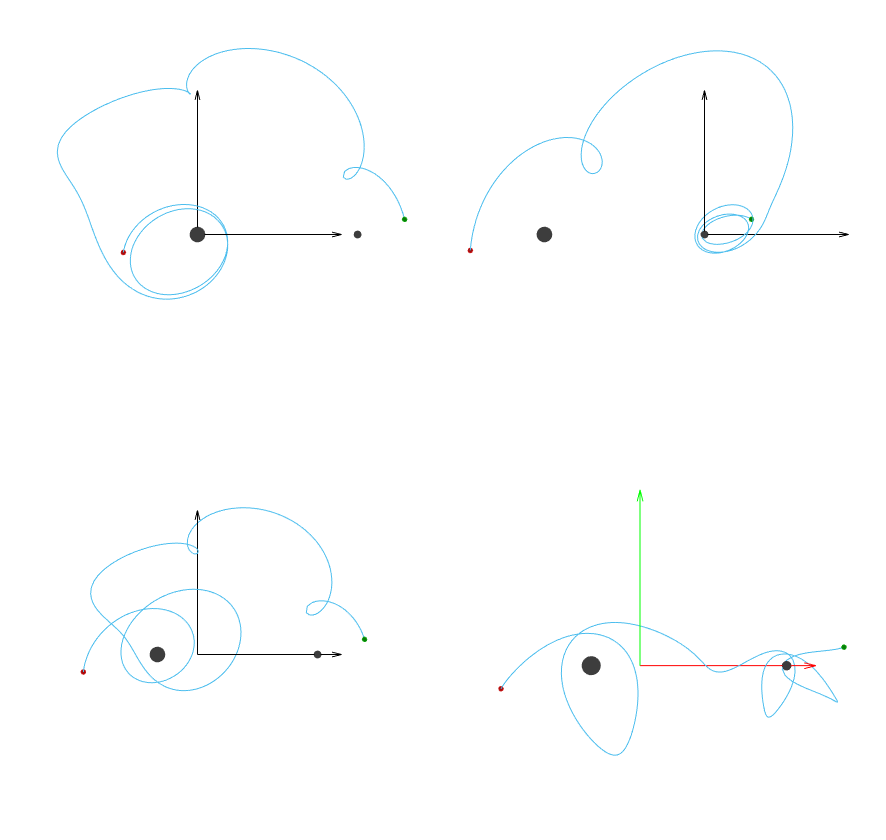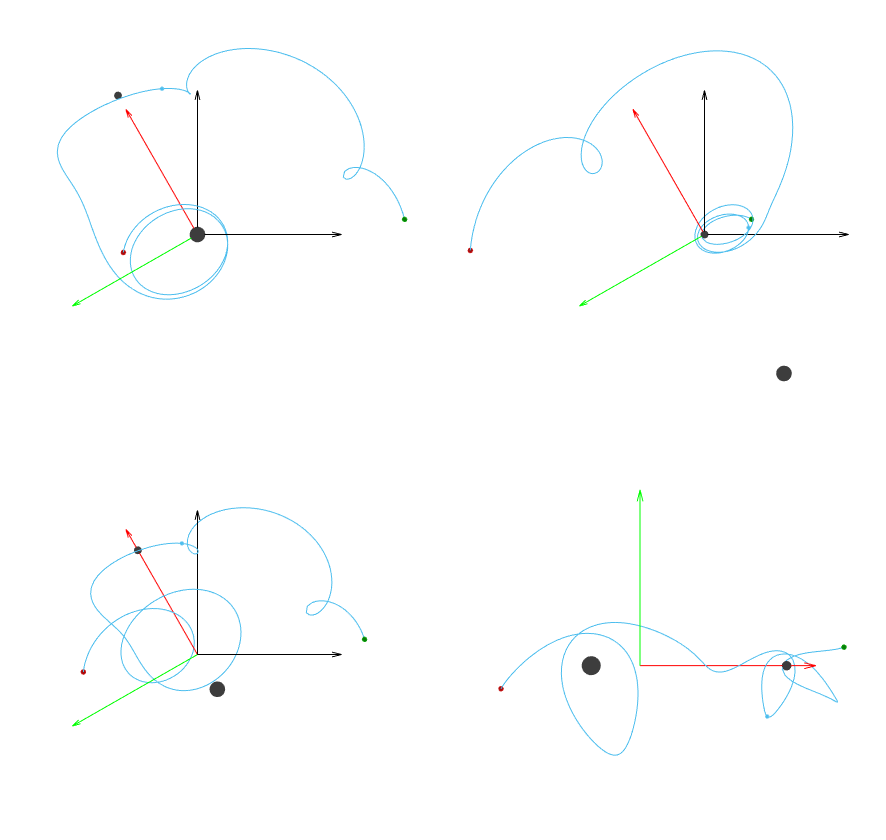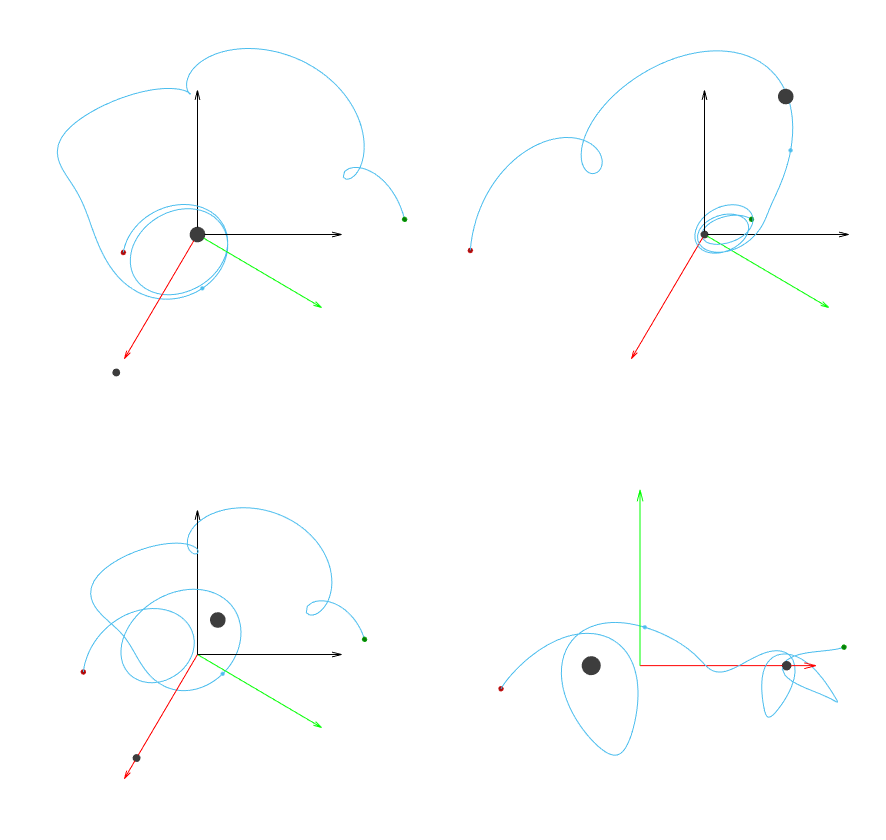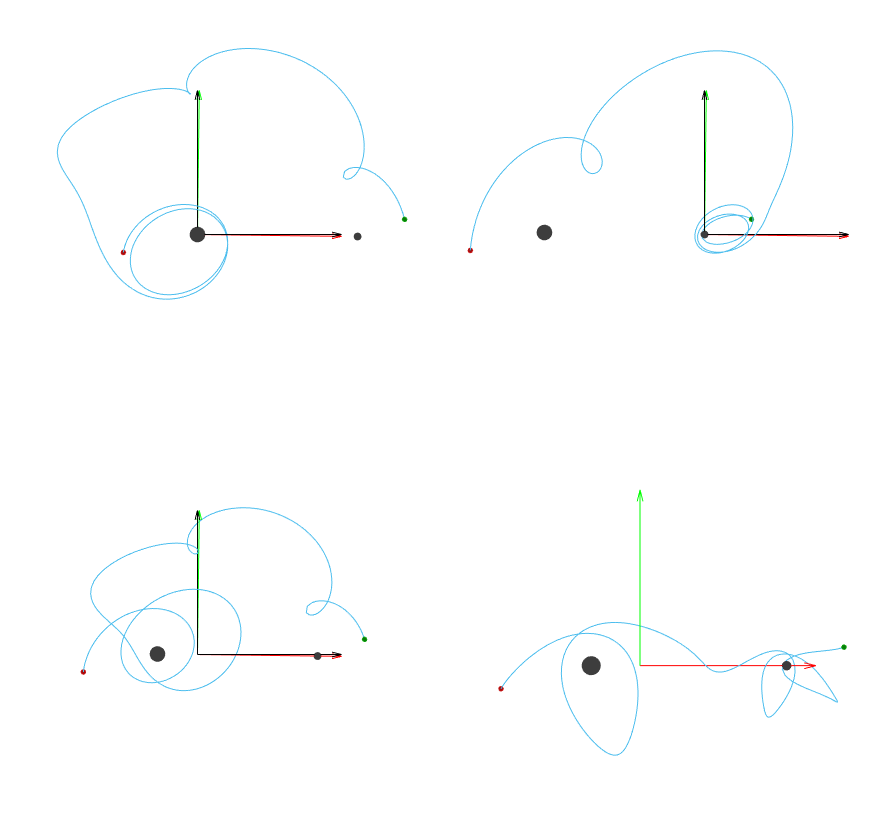
Fig. 4 Inertial frame relative to the primary (top left) and secondary (top right). Inertial frame relative to the barycenter (bottom left) and rotating frame at the barycenter (bottom right).

Note

The location of the inertial frame’s origin affects what the resulting trajectory looks like; however, shifting the origin to a different location in the rotating frame doesn’t change the trajectory qualitatively since the coordinate transformation is constant.

Comparison to ECI and ECEF

Managing the inertial frame and rotating frame in the CRTBP is actually not so different from two frames that get commonly used in astrodynamics: ECI and ECEF.

Very simply, ECI is directly comparable to the CRTBP’s inertial frame because both are inertial frames.

• This means that both frames are always pointing in constant directions

Similarly, ECEF is directly comparable to the CRTBP’s rotating frame because they’re both fundamentally rotating frames and therefore perform the same duty of removing time-dependence from the rotation.

• This is true even despite them having different roles as rotating frames (ECEF being body-fixed vs. the CRTBP rotating frame keeping both bodies aligned on one axis)

Fig. 5 The particle’s motion is traced out by both black (ECI) and yellow (ECEF) curves.

Note how ECEF rotates with the Earth by definition, so a single snapshot of the yellow trajectory fully describes the particle’s motion relative to the Earth’s surface. This is completely analogous to how desirable it is to work with CRTBP trajectories in the rotating frame.